Toroidal Constraints for Two Point Localization Under High Outlier Ratios
2017
Conference Paper
avg
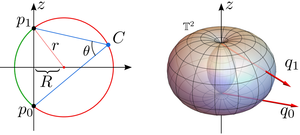
Localizing a query image against a 3D model at large scale is a hard problem, since 2D-3D matches become more and more ambiguous as the model size increases. This creates a need for pose estimation strategies that can handle very low inlier ratios. In this paper, we draw new insights on the geometric information available from the 2D-3D matching process. As modern descriptors are not invariant against large variations in viewpoint, we are able to find the rays in space used to triangulate a given point that are closest to a query descriptor. It is well known that two correspondences constrain the camera to lie on the surface of a torus. Adding the knowledge of direction of triangulation, we are able to approximate the position of the camera from \emphtwo matches alone. We derive a geometric solver that can compute this position in under 1 microsecond. Using this solver, we propose a simple yet powerful outlier filter which scales quadratically in the number of matches. We validate the accuracy of our solver and demonstrate the usefulness of our method in real world settings.
| Author(s): | Federico Camposeco and Torsten Sattler and Andrea Cohen and Andreas Geiger and Marc Pollefeys |
| Book Title: | Proceedings IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017 |
| Year: | 2017 |
| Month: | July |
| Day: | 21-26 |
| Publisher: | IEEE |
| Department(s): | Autonomous Vision |
| Research Project(s): |
Global Localization and Affordance Learning
|
| Bibtex Type: | Conference Paper (inproceedings) |
| Paper Type: | Conference |
| Event Name: | IEEE Conference on Computer Vision and Pattern Recognition (CVPR) |
| Event Place: | Honolulu, HI, USA |
| Address: | Piscataway, NJ, USA |
| ISBN: | 978-1-5386-0457-1 |
| ISSN: | 1063-6919 |
| Links: |
pdf
suppmat Project Page |
| Attachments: | |
|
BibTex @inproceedings{Camposeco2017CVPR,
title = {Toroidal Constraints for Two Point Localization Under High Outlier Ratios},
author = {Camposeco, Federico and Sattler, Torsten and Cohen, Andrea and Geiger, Andreas and Pollefeys, Marc},
booktitle = {Proceedings IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017},
publisher = {IEEE},
address = {Piscataway, NJ, USA},
month = jul,
year = {2017},
doi = {},
month_numeric = {7}
}
|
|